밑바닥부터 시작하는 딥러닝 5장 10. 시그모이드 계층 구현하기

밑바닥부터 시작하는 딥러닝 책 참고 

목차 

1. 시그모이드 함수란 

2. 시그모이드 계층 수학식 

3. 시그모이드 계층 클래스 생성 코드 (파이썬)

4. 시그모이드 클래스 객체화 시켜보기 

 

 

1. 시그모이드(sigmoid) 함수란 

시그모이드 함수는 0~1 사이의 함수이며, 입력값을 받아서 0~1 사이의 실수로 값을 반환하는 활성화 함수이다. 

연속형 데이터이기 때문에 계단 함수가 끊기지 않는 매끄러운 모양으로 바뀐 것을 알 수 있다.

동시에 이상치가 들어온다 할지라도, 시그모이드 함수는 0과 1에 수렴하므로, 이상치 문제도 해결하면서, 연속된 값을 전달할 수 있다. 

시그모이드 함수를 활성화 함수로 사용하면, 0과 1에 가까운 값을 통해 이진분류를 할 수 있다. 

(출력 값이 어느 값에 가까운지를 통해 어느 분류에 속하는지 쉽게 알 수 있다.)

시그모이드 활성화 함수

출처: 딥러닝-3.1. 활성화함수(2)-시그모이드 함수(Sigmoid) (tistory.com)

2. 시그모이드(Sigmoid) 계층 

시그모이드 함수는 다음 식을 의미하는 함수이다.

시그모이드 수식

이 수학식을 계산 그래프로 그리면 다음과 같다 

시그모이드 계층의 계산 그래프(순전파)

시그모이드 계산 그래프(순전파) [그림 5-19]

위 그림에서 'x' 와 '+' 노드 말고도 'exp'와 '/' 노드가 새롭게 등장했다.

'exp' 노드는 y=exp(x) 계산을 수행하고 '/' 노드는 y=1/x 계산을 수행한다. 

 

이제 이 순전파를 오른쪽부터 왼쪽으로 한단계씩 역전파하는 과정을 보겠다.

우선 순전파에서 중요한 값은 x 이지만, 역전파에서 중요한 값은 y이다.

그래서 역전파에서는 x를 y에 대한 식으로 치환한다. 

 

1단계 

'/' 노드, 즉 y=1/x 을 미분하면 다음식이 된다.

역전파 때는 상류에서 흘러온 값에 -y² 을 곱해서 하류로 전달

 

2단계

'+' 노드는 상류에서 흘러온 값을 여과없이 하류로 보내므로 1단계 역전파와 같다.

 

3단계

3단계까지의 역전파 그래프

'exp'노드는 y=exp(x) 연산을 수행하며, 그 미분은 똑같이 exp(x) 이다.

그럼 계산 그래프에서 2단계의 값에(상류의 값) exp(-x) (왜냐면 여기서는 순저파 값이 exp(-x)이므로) 을 곱해 

하류로 전달한다.

 

4단계 

4단계까지의 역전파 그림

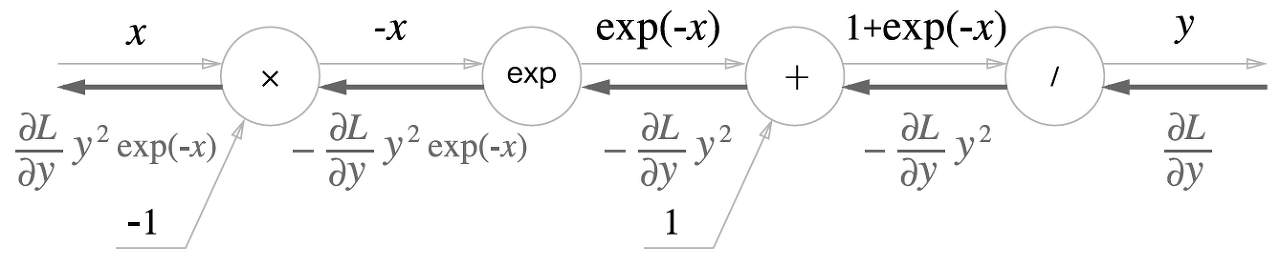
'x' 노드는 순전파 때의 값을 '서로 바꿔' 곱한다. 여기서는 -1(상대편 순전파값)을 곱한다.

 

마지막 값을 정리하면 (aL/ay)*y(1-y) 가 된다.

 

 

 

3. 시그모이드(Sigmoid) 계층 클래스 생성 코드

class Sigmoid:  # 시그모이드 클래스 
    def __init__(self):
        self.out=None
    
    def forward(self,x):
        out= 1/(1+np.exp(-x)) # 0~1 사이 실수(확률) 출력하는 함수 y=1/1+(e)-x
        self.out = out
        
        return out
    
    def backward(self,dout):
        dx= dout*(1.0 - self.out)*self.out   # dout : 상류층 도함수 (aL/ay)
                                             # dout*순전파의 출력 도함수(y'=(1-y)y)
                                             # dout*(1-y)y
        
        return dx

 

궁금한 것 : 왜 self.out 을 하는데 x가 아니라 y가 나오지?

4. 시그모이드 클래스 객체화 시키기 

sigmoid=Sigmoid()
x=np.array( [24 , 32, 5])
sigmoid.forward(x)

 

array([1. , 1. , 0.99330715])